力扣热题100总结

算法
hot100
笔试

TIP

近日在 LeetCode 做算法题目，以热题 100 为主 (opens new window)。因此，先过一遍其中的题目，接着对题目进行慢慢记录和总结。

记录计划如下：

不熟悉的题目/题型
题型及该类型的做题切入口
常用Java接口/技巧
笔试遇到过的题型

# 前述

不熟悉的题目：

题目	难点	关键
环形链表II (opens new window)	1）直观（朴素）做法是使用集合 `HashSet` 存放遍历过的每一个结点，同时判断该结点是否已在集合中，若存在，则说明找到循环入口； 2）进阶做法需要先做一些推理，使用两个指针 `TO(1)` 来解决问题，有一定难度。	快慢指针
盛最多水的容器 (opens new window)	总觉得这题跟柱状图中最大的矩形 (opens new window) 和接雨水 (opens new window) 很像，找到相似原因	确认双向信息

题单：

题型	切入口
滑动窗口 (opens new window)	- 无重复字符的最长子串 (opens new window) - 滑动窗口最大值 (opens new window) - 找到字符串中所有字母异位词 (opens new window)
二分查找 (opens new window)	- 搜索插入位置 (opens new window) - 在排序数组中查找元素的第一个和最后一个位置 (opens new window) - 寻找旋转排序数组中的最小值 (opens new window)
图论 (opens new window)	- 课程表 (opens new window) - 网络延迟时间 (opens new window) - 阈值距离内邻居最少的城市 (opens new window) - 设计可以求最短路径的图类 (opens new window)
动态规划 (opens new window)	- 01背包 (opens new window) - 完全背包问题 (opens new window) - 多重背包问题 II (opens new window) - 打家劫舍 (opens new window) - 完全平方数 (opens new window) - 最长回文子串 (opens new window) - 编辑距离 (opens new window)

热题100,哈希+双指针+滑动窗口+子串

# Java 算法常用

/**
 * 引入
 */
import java.util.*;  // scanner | 

/**
 * 输出较多时，先保存再统一输出
 */
StringBuilder sb = new StringBuilder();
sb.append(str);
System.out.println(sb.toString());

/**
 * 数组常用函数
 */
int[] a = new int[n];
Arrays.fill(a, -1);    // 填充
Arrays.sort(a);        // 排序

/****************** 常用对象 ******************/

/**
 * 队列 | 栈
 */
Deque<Integer> deque = new ArrayDeque<>()
deque.offer(element); // 入队
int a = deque.poll(); // 出队
deque.push(element);  // 入栈
int a = deque.pop();  // 出栈
int a = deque.peek(); // 查看栈顶/队头元素，不删除       

/**
 * 优先队列
 */
// 小顶堆
PriorityQueue<Integer> pq = new PriorityQueue<>();  // 默认情况
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (a[0] - b[0]));
// 大顶堆
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (b[0] - a[0]));
PriorityQueue<Integer> pq = new PriorityQueue<>Comparator.reverseOrder());

/**
 * 邻接表
 */
List<int[]>[] g = new ArrayList[n];          // g[ui].get(j) = {vi, wi}
Arrays.setAll(g, r -> new ArrayList<>());
// 构建邻接表
for (int[] adj : adjs) g[adj[0]].add(new int[]{adj[1], adj[2]});

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

# 笔记&模板

# 二分查找

目前最容易理解二分查找的办法是 红蓝染色法。我们以问题为导向来讲解该方法。

# 问题

题例

给定一个从小到大有序的数组 nums，以及一个目标值 x。从数组 nums 中找出从左到右第一个大于等于 x 的元素 nums[j]，返回该元素的下标 j 。

# 解决方法

方法1：暴力

暴力做法很容易理解，就是从左到右遍历数组，比较每个元素 nums[i] 与目标值 x 的大小，如果符合题目条件，就返回当前下标。

public static void find(int[] nums, int x){
  for (int i = 0; i < nums.length; ++ i ) {
    if (nums[i] >= x) return i;  // 找到时，返回下标
  }
  return -1;                     // 找不到时返回 -1
}

1
2
3
4
5
6

因为要遍历整个数组，其时间复杂度为 $O(n)$ .

方法2：二分

仔细想一想，方法1的做法在任何数组上都可以执行，并没有利用到“数组有序”这个性质。

那该怎么利用这个性质呢？这就是接下来的二分查找：

利用两个指针 l 和 r 分别指向数组 nums 的「不确定区间」的两端，该「不确定区间」内的数都是还未确定与 x 的大小关系。

通过两个指针的中间指针 mid = l + (r - l) / 2 所指向的元素 nums[mid] 与目标值 x 进行比较，可以确认「不确定区间」中一半元素与 x 的大小关系，从而不断缩小「不确定区间」的大小，最终将整个数组分离成「< x 区间」和「>= x 区间」。

上面这段话挺绕的，如果看不明白，先接着往下看，我们从示例一步步演示。

🟫 示例：nums = {5, 7, 7, 8, 8, 10}, x = 8.

最重要的是 「不确定区间」的定义：该区间内的数/元素都还未确定与 x 的大小关系。

很明显，在「不确定区间」外的元素都是确定了与 x 的大小关系。为了更加形象，我们规定：在「不确定区间」外，将小于 x 的元素染成红色，将大于等于 x 的元素染成蓝色。

【第一轮】整个数组 [0, 5] 都是「不确定区间」，所以都还没染色
- 指针 l = 0、r = 5、mid = 2
- nums[mid] = 7 与 x = 8 比较，得到 nums[mid] < x
- 从比较结果与“数组有序”的性质可以知道，区间 [l, mid] => [0, 2] 的元素都是小于 x，可以给该区间染上红色
- 区间变成：{5, 7, 7, 8, 8, 10}
- 此时「不确定区间」变成 {8, 8, 10} ，所以要更新左端点指针 l = mid + 1 = 3（因为两个指针是用来指向「不确定区间」的两端）如下图所示

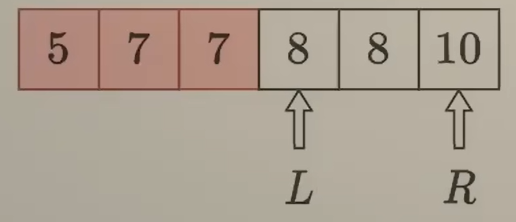
【第二轮】l <= r，所以「不确定区间」是 [3, 5]
- 指针 l = 3、r = 5、mid = 4
- nums[mid] = 8 与 x = 8 比较，得到 nums[mid] == x
- 从比较结果与“数组有序”的性质可以知道，区间 [mid, r] => [4, 5] 的元素都是大于等于 x，可以给该区间染上蓝色
- 区间变成：{5, 7, 7, 8, 8, 10}
- 此时「不确定区间」变成 {8} ，所以要更新右端点指针 r = mid - 1 = 3

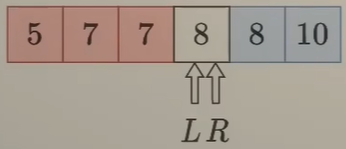
【第三轮】l <= r，所以「不确定区间」是 [3, 3]
- 指针 l = 3、r = 3、mid = 3
- nums[mid] = 8 与 x = 8 比较，得到 nums[mid] == x
- 从比较结果与“数组有序”的性质可以知道，区间 [mid, r] => [3, 3] 的元素都是大于等于 x，可以给该区间染上蓝色
- 区间变成：{5, 7, 7, 8, 8, 10}
- 此时已经没有「不确定区间」，但仍然按照规则更新右端点指针 r = mid - 1 = 2

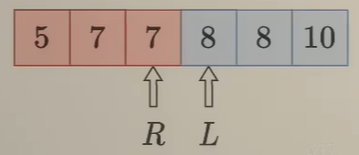
【第四轮】l > r，所以没有「不确定区间」了，已经将整个数组分离成「< x 区间」和「>= x 区间」，停止循环。停下来后有几个特性（如上图所示）：
- 红色在整个区间的左边，蓝色在整个区间的右边，所谓“二分”
- l > r，并且l 指向的是蓝色部分的第一个元素，r 指向的是红色部分的最后一个元素
【最终】因为是寻找 >=x 的第一个元素，返回 l 或者 r + 1 即可。

代码：

public static void bisect_left(int[] nums, int x){
  int l = 0, r = nums.length - 1, mid;
  while (l <= r) {
    mid = l + (r - l) / 2;
    if (nums[mid] >= x) r = mid - 1;  // [mid, r] 染成蓝色
    else l = mid + 1;                 // [l, mid] 染成红色
  }
  return l; // l 要么出界了，要么指向第一个 >= x 的元素
}

1
2
3
4
5
6
7
8
9

有人可能会问：很多讲解常说的循环不变量体现在哪里？

我还是从「不确定区间」的角度去解释

在每一轮中，消灭了一半的「不确定区间」，要么左指针 l 移动到了红色区域的右边，要么右指针 r 移动到了蓝色区域的左边；
甚至在最终，l 在红色区域的右边（指向蓝色区域的第一个元素），r 在蓝色区域的左边（指向红色区域的最后一个元素）
上面两条合并起来理解，在每次比较并更新后，循环不变量体现在这里：
- l 和 r 始终指向「不确定区间」的两端
- l 始终在红色区域的右边，r 始终在蓝色区域的左边

这些信息，也可以从示例的三张图可以看出来。

DANGER

注：以上的讲解均以左闭右闭区间为例

# 模板

# 三种写法

求 $\ge x$ 的情况，可以使用以下3种写法之一的二分查找：

// 写法1：闭区间，即 [l, r] 是「不确定区间」
public static void bisect_left(int[] nums, int x){
  int l = 0, r = nums.length - 1, mid;
  while (l <= r) {
    mid = l + (r - l) / 2;
    if (nums[mid] >= x) r = mid - 1;  // [mid, r] 染成蓝色
    else l = mid + 1;                 // [l, mid] 染成红色
  }
  // l 要么出界了，要么指向第一个 >= x 的元素
  return l;  // or r+1
}


// 写法2：左闭右开区间，即 [l, r) 是「不确定区间」（不包括右边界r）
public static void bisect_left(int[] nums, int x){
  int l = 0, r = nums.length, mid;
  while (l < r) {
    mid = l + (r - l) / 2;
    if (nums[mid] >= x) r = mid;
    else l = mid + 1;
  }
  return l;  // or r
}

// 写法3：开区间，即 (l, r) 是「不确定区间」（不包括左右边界l和r）
public static void bisect_left(int[] nums, int x){
  int l = -1, r = nums.length, mid;
  while (l + 1 < r) {
    mid = l + (r - l) / 2;
    if (nums[mid] >= x) r = mid;
    else l = mid;
  }
  return r; // or l+1
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

对于整数来说，如果求 $\gt x$ or $\lt x$ or $\le x$ 的情况，可以变通一下使用上面的函数：

bisect_left(nums, x + 1);  // 求 > x

bisect_left(nums, x) - 1;  // 求 < x

bisect_left(nums, x + 1) - 1;  // 求 <= x

1
2
3
4
5

# 复杂度分析

复杂度分析
时间复杂度	$O(\log{n})$
空间复杂度	$O(1)$

# 同类题型

灵茶山艾府 | 分享丨【题单】二分算法（二分答案/最小化最大值/最大化最小值/第K小） (opens new window)

二分的关键

总结下来的几个关键点：

二分因「不确定区间」的存在而开始
二分时，关键不在于区间里的元素具有什么性质，而是区间外面的元素具有什么性质，并用指针牢牢指向「不确定区间」的两端
二分时，如何判断当前位置是染成红色还是蓝色
二分因「不确定区间」的消除而结束（最终划分成红色和蓝色区间）

做类似题目时的思考切入点：

二分的是什么？ 时间 / 最大值 / ...
怎么二分？ check()函数的写法
二分的边界怎么确定？ 时间的最小（大）值 / ...

【二分查找】

34. 在排序数组中查找元素的第一个和最后一个位置 (opens new window)
35. 搜索插入位置 (opens new window)
704. 二分查找 (opens new window)
2529. 正整数和负整数的最大计数 (opens new window)
2300. 咒语和药水的成功对数 (opens new window)
- $\lceil \frac{a}{b} \rceil = \lfloor \frac{a + b - 1}{b} \rfloor = \lfloor \frac{a - 1}{b} \rfloor + 1$
2563. 统计公平数对的数目 (opens new window)
- $l \le a[i] + a[j] \le u \Rightarrow l - a[j] \le a[i] \le u - a[j]$

【二分答案】

【最小化最大值】

410. 分割数组的最大值 (opens new window)

# 最短路算法

关于最短路算法，可以这样区分：

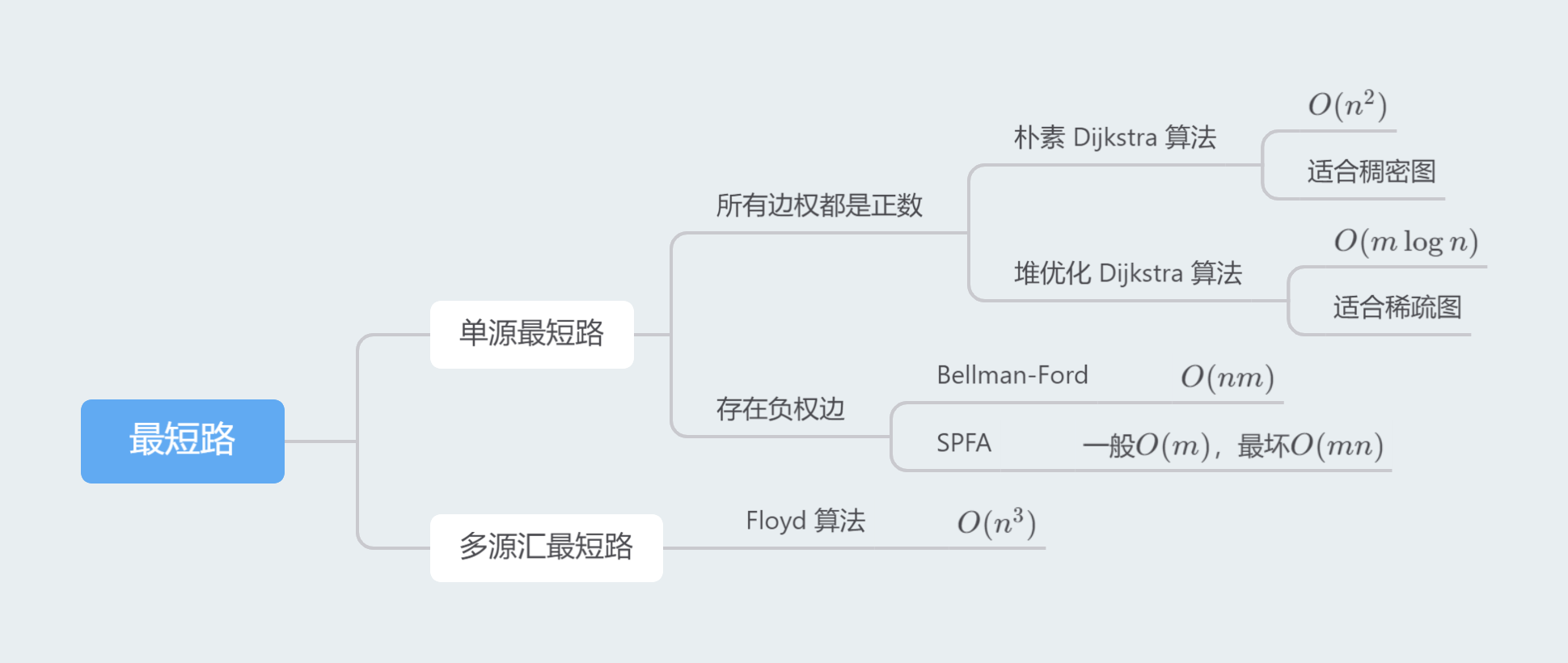
题例：743. 网络延迟时间

有 n 个网络节点，标记为 1 到 n。

给你一个列表 times，表示信号经过有向边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。

现在，从某个节点 k 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1 。

提示：

1 <= k <= n <= 100
1 <= times.length <= 6000
times[i].length == 3
1 <= ui, vi <= n
ui != vi
0 <= wi <= 100
所有 (ui, vi) 对都互不相同（即，不含重复边）

From LeetCode (opens new window)

# Dijkstra 算法

Dijkstra 是「单源最短路」算法。

# 算法思想

定义 $g[i][j]$ 表示节点 $i$ 到节点 $j$ 这条边的边权。如果没有 $i$ 到 $j$ 的边，则 $g[i][j] = \infty$ 。

定义 $\textit{dist}[i]$ 表示节点 $k$ 到节点 $i$ 的最短路长度，一开始 $\textit{dist}[k]=0$ ，其余 $\textit{dist}[i] = \infty$ 表示尚未计算出。

我们的目标是计算出最终的 $dist$ 数组。

首先更新节点 $k$ 到其邻居 $k$ 的最短路，即更新 $\textit{dist}[y]$ 为 $g[k][y]$ 。
然后取除了节点 $k$ 以外的 $\textit{dist}[i]$ 的最小值，假设最小值对应的节点是 $3$ 。此时可以断言： $\textit{dist}[3]$ 已经是 $k$ 到 $3$ 的最短路长度，不可能有其它 $k$ 到 $3$ 的路径更短！反证法：假设存在更短的路径，那我们一定会从 $k$ 出发经过一个点 $u$ ，它的 $dist[u]$ 比 $\textit{dist}[3]$ 还要小，然后再经过一些边到达 $3$ ，得到更小的 $\textit{dist}[3]$ 。但 $\textit{dist}[3]$ 已经是最小的了，并且图中没有负数边权，所以 $u$ 是不存在的，矛盾。故原命题成立，此时我们得到了 $\textit{dist}[3]$ 的最终值。
用节点 $3$ 到其邻居 $y$ 的边权 $g[3][y]$ 更新 $\textit{dist}[y]$ ：如果 $\textit{dist}[3]+g[3][y] < \textit{dist}[y]$ ，那么更新 $\textit{dist}[y]$ 为 $\textit{dist}[3]+g[3][y]$ ，否则不更新。
然后取除了节点 $k,3$ 以外的 $\textit{dist}[i]$ 的最小值，重复上述过程。
由数学归纳法可知，这一做法可以得到每个点的最短路。当所有点的最短路都已确定时，算法结束。

# 朴素 Dijkstra （适用于稠密图）

当边的数量远远大于节点数时，就可以认定为稠密图（其实有相对严谨的稠密图/稀疏图定义，但我懒得查了）。此时可以用邻接矩阵来表示节点的邻接关系。

稠密图：边数较多，边数接近于点数的平方，即 $m \approx n^2$
稀疏图，边数较少，边数接近于点数，即 $m \approx n$

# 模板

    /**
        Dijkstra 算法 —— 单源最短路算法
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
          k:     从节点 k 出发        0 <= k <= n - 1
        返回值：
          dist:  最短距离数组
     */
    private int[] dijkstra(int[][] adjs, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2; // 防止加法溢出

        // 邻接矩阵
        int[][] g = new int[n][n];
        for (int[] row : g) Arrays.fill(row, INF);
        // 构建邻接矩阵
        for (int[] adj : adjs) g[adj[0]][adj[1]] = adj[2];  

        int[] dist = new int[n];           // dist[i] 表示 k 到 i 的最短路长度
        boolean[] fixed = new boolean[n];  // fixed[i] = true 表示 dist[i] 已确定最短路长度，无需再计算

        // 初始化 dist 数组
        Arrays.fill(dist, INF);
        dist[k] = 0;

        // 一共 n 个节点，需要循环 n-1 次来更新 n-1 个 dist
        int m = n - 1;
        while (m -- > 0) {
            // 1）取 fixed = true 之外的 dist 的最小值
            int t = -1;
            for (int j = 0; j < n; ++ j ) {
                if (!fixed[j] && (t == -1 || dist[j] < dist[t])) t = j;
            }

            if (dist[t] == INF) {
              System.out.println("存在无法到达的节点：" + t);
            }
            
            fixed[t] = true;  // 2）确定 dist[t] 的最短路长度

            // 3）用节点 t 到其邻接 y 的边权 g[t][y] 更新 dist
            for (int y = 0; y < n; ++ y ) dist[y] = Math.min(dist[y], dist[t] + g[t][y]);
        }

        return dist;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

# 复杂度分析

复杂度分析
时间复杂度	$O(n^2)$
空间复杂度	$O(n^2)$

# 堆优化 Dijkstra （适用于稀疏图）

寻找最小值的过程可以用一个最小堆来快速完成：

一开始把 $(\textit{dist}[k], k)$ 二元组入堆。
当节点 $x$ 首次出堆时， $\textit{dist}[x]$ 就是写法一中寻找的最小最短路。
更新 $\textit{dist}[y]$ 时，把 $(\textit{dist}[y],y)$ 二元组入堆。

# 模板

    /**
        Dijkstra 算法（堆优化版） —— 单源最短路算法
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
          k:     从节点 k 出发        0 <= k <= n - 1
        返回值：
          dist:  最短距离数组
     */
    private int[] dijkstra_heap(int[][] adjs, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2; // 防止加法溢出

        // 邻接表
        List<int[]>[] g = new ArrayList[n];          // g[ui].get(j) = {vi, wi}
        Arrays.setAll(g, r -> new ArrayList<>());
        // 构建邻接表
        for (int[] adj : adjs) g[adj[0]].add(new int[]{adj[1], adj[2]});

        int[] dist = new int[n];           // dist[i] 表示 k 到 i 的最短路长度
        boolean[] fixed = new boolean[n];  // fixed[i] = true 表示 dist[i] 已确定最短路长度，无需再计算

        // 初始化 dist 数组
        Arrays.fill(dist, INF);
        dist[k] = 0;

        // 优先队列/小顶堆
        PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (a[0] - b[0]));  // 元素：{distance, node}，优先按距离排序 
        pq.offer(new int[]{0, k});   // {0, k} 入队，k 是开始节点

        // 队列不空，还可能有更新
        while (!pq.isEmpty()) {
            int[] s = pq.poll();    // 1）取 fixed = true 之外的 dist 的最小值
            int d = s[0], t = s[1];
            
            if (fixed[t]) continue;  // t 在之前已确定（跳过 fixed = true 的节点）

            fixed[t] = true;         // 2）确定 dist[t] 的最短路长度

            // 3）用节点 t 到其邻接 y 的边权 g[t][y] 更新 dist
            for (int[] e : g[t]) {
                int y = e[0], w = e[1];
                if (d + w < dist[y]) {
                    dist[y] = d + w;
                    pq.offer(new int[]{dist[y], y});
                }
            }
        }

        return dist;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

# 复杂度分析

复杂度分析
时间复杂度	$O(m \log m)$ , 其中 $m$ 为 $\textit{adjs}$ 的长度。由于 $m \ge n-1$ ，分析复杂度时以 $m$ 为主。
空间复杂度	$O(m)$

# Bellman Ford

Dijkstra 不能解决负权边，是因为 Dijkstra 要求每个点被确定后设置 fixed[j] = true 、 dist[j] 就是最短距离了，之后就不能再被更新了。而如果有负权边的话，那已经确定的点的 dist[j] 不一定是最短了。

TIP

松弛操作：以 a 为起点，b 为终点，ab 边长度为 w 为例。dist[a] 代表源点 s 到 a 点的路径长度，dist[b] 代表源点 s 到 b 点的路径长度。如果满足下面的式子则将 dist[b] 更新为 dist[a] + w。

BF判断负权回路：在正常情况下，BF 进行 $n-1$ 次遍历，每次遍历对所有边进行松弛操作。遍历都结束后，此时源点 s 到其余点 b 的最短路已经找到。若再进行一次遍历，还能得到 s 到某些节点更短的路径的话，则说明存在负权回路。

# 模板

    // 边类
    class Edge {
        int a, b, w;
        Edge(int a, int b, int w) {
            this.a = a;  this.b = b;  this.w = w;
        }
    }
    /**
        bellman ford 算法 —— 单源最短路算法
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
          k:     从节点 k 出发        0 <= k <= n - 1
        返回值：
          dist:  最短距离数组
     */
    private int[] bellmanFord(int[][] adjs, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2; // 防止加法溢出

        // 邻接关系
        List<Edge> edges = new ArrayList<>();
        for (int[] adj : adjs) {
            int a = adj[0], b = adj[1], w = adj[2];
            edges.add(new Edge(a, b, w));
        }

        int[] dist = new int[n];           // dist[i] 表示 k 到 i 的最短路长度

        // 初始化 dist 数组
        Arrays.fill(dist, INF);
        dist[k] = 0;

        // 统计经过 i 条边所能到达的节点的值，（不存在负权回路的情况下）最多经过 n-1 条边找到最短路
        for (int i = 0; i < n; ++ i ) {
            int[] backup = dist.clone();  // 复制
            // 更新，每次都使用上一次迭代的结果，执行松弛操作
            for (Edge e : edges) {
                int a = e.a, b = e.b, w = e.w;
                dist[b] = Math.min(dist[b], backup[a] + w);
            }
        }

        return dist;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# 复杂度分析

复杂度分析
时间复杂度	$O(nm)$
空间复杂度	$O(m)$

# SPFA（BF 优先队列优化）

SPFA 是对 Bellman Ford 的优化实现，可以使用队列进行优化，也可以使用栈进行优化。

# 模板

    /**
        SPFA 算法 —— 单源最短路算法
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
          k:     从节点 k 出发        0 <= k <= n - 1
        返回值：
          dist:  最短距离数组
     */
    private int[] spfa(int[][] adjs, int n, int k) {
        final int INF = Integer.MAX_VALUE / 2; // 防止加法溢出

        // 邻接表
        List<int[]>[] g = new ArrayList[n];
        Arrays.setAll(g, r -> new ArrayList<>());
        // 构建邻接表
        for (int[] adj : adjs) g[adj[0]].add(new int[]{adj[1], adj[2]});

        int[] dist = new int[n];           // dist[i] 表示 k 到 i 的最短路长度
        boolean[] fixed = new boolean[n];  // 标记节点 i 「是否入队」

        // 初始化 dist 数组
        Arrays.fill(dist, INF);
        dist[k] = 0;
        fixed[k] = true;

        // 使用队列存储节点，起点是节点 k
        Deque<Integer> que = new ArrayDeque<>();
        que.offer(k);
        while (!que.isEmpty()) {
            // 每次从队列中取出，并标记「未入队」
            int t = que.poll();  
            fixed[t] = false;
            // 尝试使用该点，更新其他点的最短距离
            // 如果更新的点，本身「未入队」则加入队列中，并标记「已入队」
            for (int[] e : g[t]) {
                int y = e[0], w = e[1];
                if (dist[t] + w < dist[y]) {
                    dist[y] = dist[t] + w;
                    if (!fixed[y]) {
                        que.offer(y);
                        fixed[y] = true;
                    }
                }
            }
        }

        return dist;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

SPFA 判断负权回路模板

这里的关键在于：在不存在负权回路的情况下，两个节点之间的最短路径最多包含 $n-1$ 个节点。若源点 $k$ 到达某个节点 $i$ 的路径包含 $n$ 个节点以上，说明最短路走了一个回路，而要包含回路，肯定是这个回路的权重小于 $0$ 。因此，我们要判断 $k$ 到每个节点 $i$ 的最短路节点数 $\textit{cnt}[i]$ 是否大于 $n$ ，若大于，则存在负权回路。

但是需要注意的是，这里的源点是虚拟节点 $k \ \ (k \notin [0,n-1])$ ，从该点向其他所有点连一条权值为 $0$ 的有向边。加入虚拟节点也有另一个含义：如果原本的图不是连通的，加入虚拟节点后，可以使得这个图连通。

下面是使用 SPFA 判断负权回路的模板，高亮部分是与 SPFA 模板不同的地方，主要不同：

初始化 $\textit{dist}$ 为 $0$ 。（SPFA 是 INF）
初始队列时，所有节点入队。（SPFA 是 que.offer(k)）
增加 $\textit{cnt}$ 数组表示最短路的节点数量。（SPFA 不需要）

    /**
        SPFA 算法 判断是否存在负权回路
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
        返回值：
          boolean 是否存在负权回路
     */
    private boolean spfa(int[][] adjs, int n) {
        // final int INF = Integer.MAX_VALUE / 2; // 防止加法溢出

        // 邻接表
        List<int[]>[] g = new ArrayList[n];
        Arrays.setAll(g, r -> new ArrayList<>());
        // 构建邻接表
        for (int[] adj : adjs) g[adj[0]].add(new int[]{adj[1], adj[2]});

        int[] dist = new int[n];           // dist[i] 表示 k 到 i 的最短路长度
        int[] cnt = new int[n];            // 表示「虚拟源点」 k 到节点 i 的最短路节点数量
        boolean[] fixed = new boolean[n];  // 标记节点 i 「是否入队」

        // 初始化 dist 数组，假设「虚拟源点」 k 到所有节点的权重为 0 (并不是真实存在)
        Arrays.fill(dist, 0);

        // 使用队列存储节点，起点是「虚拟源点」 k 连接的所有节点
        Deque<Integer> que = new ArrayDeque<>();
        for (int i = 0; i < n; ++ i ) {
            que.offer(i);
            fixed[i] = true;
        }
        
        while (!que.isEmpty()) {
            // 每次从队列中取出，并标记「未入队」
            int t = que.poll();  
            fixed[t] = false;
            // 尝试使用该点，更新其他点的最短距离
            // 如果更新的点，本身「未入队」则加入队列中，并标记「已入队」
            for (int[] e : g[t]) {
                int y = e[0], w = e[1];
                if (dist[t] + w < dist[y]) {
                    dist[y] = dist[t] + w;
                    cnt[y] = cnt[t] + 1;  // 更新最短路节点数量
                    if (cnt[y] >= n) {    // 存在负权回路
                        System.out.println("存在负权回路");
                        return true;  
                    }
                    if (!fixed[y]) {
                        que.offer(y);
                        fixed[y] = true;
                    }
                }
            }
        }

        return false;  // 能顺利退出循环，说明不存在负权回路
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56

# 复杂度分析

复杂度分析
时间复杂度	通常情况下为 $O(km)$ ， $k$ 一般为 $4$ 到 $5$ ，最坏情况下（当数据为网格图时）为 $O(nm)$
空间复杂度	$O(n^2)$

# Floyd 算法

Floyd 是「多源汇最短路」算法。

# 算法思想

Floyd 算法基于动态规划，其原始三维状态定义为 $\textit{dist}[p][i][j]$ ，表示「所有从点 $i$ 到点 $j$ ，且允许经过点集 $(1,...,p)$ 的「路径」中的最短距离。

状态转移方程：

\textit{dist}[p][i][j] = \min(\textit{dist}[p - 1][i][j], \textit{dist}[p - 1][i][p] + \textit{dist}[p - 1][p][j])

上式中， $\textit{dist}[p - 1][i][j]$ 代表从 $i$ 到 $j$ 但必然不经过点 $p$ 的路径， $\textit{dist}[p−1][i][p]+\textit{dist}[p−1][p][j]$ 代表必然经过点 $p$ 的路径，两者中取较小值更新 $\textit{dist}[p][i][j]$ 。

不难发现，任意的 $\textit{dist}[p][X][Y]$ 依赖于 $\textit{dist}[p - 1][X][Y]$ ，可采用滚动数组的方式进行优化。

将 $\textit{dist}$ 声明为二维数组， $\textit{dist}[i][j]$ 代表从点 $i$ 到点 $j$ 的最短距离，并采取 “枚举中转点 - 枚举起点 - 枚举终点” 三层循环的方式更新 $\textit{dist}[i][j]$ 。

如此一来，跑一遍 Floyd 算法便可得出任意两点的最短距离。

注

Floyd 算法可以处理正负权边的图，但不能有负权回路。当然，也可以利用 Floyd 对图中负环进行判定。

# 模板

    /**
        floyd 算法
        前提：图中不存在负权回路
        g: 初始时，邻接矩阵；结束时，g[i][j] 表示节点 i 到节点 j 的最短路径距离
     */
    private void floyd(int[][] g) {
        int n = g.length;
        // floyd 基本流程为三层循环: [枚举中转点 - 枚举起点 - 枚举终点] => 松弛操作  
        for (int p = 0; p < n; ++ p ) {
            for (int i = 0; i < n; ++ i )
                for (int j = 0; j < n; ++ j )
                    g[i][j] = Math.min(g[i][j], g[i][p] + g[p][j]);
        }
        // 此时，g[i][j] 表示节点 i 到节点 j 的最短路径
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

# 复杂度分析

复杂度分析
时间复杂度	$O(n^3)$
空间复杂度	$O(n^2)$

# 同类题型

灵茶山艾府 | 分享丨【题单】图论算法（DFS/BFS/拓扑排序/最短路/最小生成树/二分图/基环树/欧拉路径） (opens new window)

【单源最短路：Dijkstra / BF / SPFA】

【全源最短路：Floyd】

# 最小生成树算法

# 题例

题例：1584. 连接所有点的最小费用

给你一个points 数组，表示 2D 平面上的一些点，其中 points[i] = [xi, yi] 。

连接点 [xi, yi] 和点 [xj, yj] 的费用为它们之间的曼哈顿距离：|xi - xj| + |yi - yj| ，其中 |val| 表示 val 的绝对值。

请你返回 将所有点连接的最小总费用。只有任意两点之间 有且仅有 一条简单路径时，才认为所有点都已连接。

From LeetCode (opens new window)

# Prim 算法

# 模板

Prim 算法的模板与单源最短路 Dijkstra 算法非常像，主要有两点不同：

第一层循环。Prim 循环 n 次，Dijkstra 循环 n - 1次。
更新距离。Prim 是 Math.min(dist[y], g[t][y])，Dijkstra 是 Math.min(dist[y], dist[t] + g[t][y])。

    /**
        Prim 算法 —— 最小生成树算法
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
        返回值：
          ans:  最小生成树的权重
     */
    private int prim(int[][] adjs, int n) {
        final int INF = Integer.MAX_VALUE / 2;

        // 邻接矩阵
        int[][] g = new int[n][n];
        for (int[] row : g) Arrays.fill(row, INF);
        // 构建邻接矩阵
        for (int[] adj : adjs) {
            int a = adj[0], b = adj[1], w = adj[2];
            g[a][b] = g[b][a] = Math.min(g[a][b], w);
        }

        int[] dist = new int[n];           // dist[i] 表示「最小生成树T」到 i 的最短路长度
        boolean[] fixed = new boolean[n];  // fixed[i] = true 表示 dist[i] 已并入「最小生成树T」，无需再计算

        // 初始化 dist 数组
        Arrays.fill(dist, INF);

        // 【注意】这里更新 n 次，因为第一次时只是先找个起点，并不算入最小距离 ans，后面 n-1 次才开始算边距
        int ans = 0;
        for (int i = 0; i < n; ++ i ) {
            // 1）取 fixed = true 之外的 dist 的最小值
            int t = -1;
            for (int j = 0; j < n; ++ j )
                if (!fixed[j] && (t == -1 || dist[j] < dist[t])) t = j;
            
            // 2）并入「最小生成树T」
            if (i != 0) ans += dist[t];  
            fixed[t] = true;

            // 3）用当前最新并入「最小生成树T」的节点更新其他节点到 T 的距离
            for (int y = 0; y < n; ++ y ) dist[y] = Math.min(dist[y], g[t][y]);  // 注意跟dijkstra的区别，这里dist保存的是到最新并入结点的距离
        }

        return ans;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

# Kruskal 算法

# 算法思想

Kruskal 算法是一种常见并且好写的 最小生成树算法，由 Kruskal 发明。该算法的基本思想是从小到大加入边，是一个 贪心算法。

其算法流程为：

将图 $G=\{V,E\}$ 中的所有边按照长度由小到大进行排序，等长的边可以按任意顺序。
初始化图 $G'$ 为 $\{V,\varnothing\}$ ，从前向后扫描排序后的边，如果扫描到的边 $e$ 在 $G'$ 中连接了两个相异的连通块,则将它插入 $G'$ 中。
最后得到的图 $G'$ 就是图 $G$ 的最小生成树。

在实际代码中，我们首先将这张完全图中的边全部提取到边集数组中，然后对所有边进行排序，从小到大进行枚举，每次贪心选边加入答案。使用并查集维护连通性，若当前边两端不连通即可选择这条边。

# 模板

# 使用 Edge 类

    
    // 边类
    class Edge implements Comparable<Edge> {
        public int x, y, w;  // 邻接点 x,y  权重 w

        public Edge(int x, int y, int w) {
            this.x = x;  this.y = y;  this.w = w;
        }

        // 内置比较器实现按 w 升序
        public int compareTo(Edge e) {
            return Integer.compare(this.w, e.w);
        }
    }

    // 并查集（查找祖先）
    private int find(int[] p, int x) {
        if (p[x] != x) p[x] = find(p, p[x]);
        return p[x];
    }

    /**
        Kruskal 算法 —— 最小生成树算法
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
        返回值：
          ans:  最小生成树的权重
     */
    private int kruskal(int[][] adjs, int n) {
        int[] p = new int[n];  // 并查集，每个节点的祖先节点（用于并查集合并操作）
        
        for (int i = 0; i < n; ++ i ) p[i] = i;  // 开始时，所有边还没合并，祖先是自己

        // 边集
        List<Edge> edges = new ArrayList<>(); 
        for (int[] adj : adjs) {
            int a = adj[0], b = adj[1], w = adj[2];
            edges.add(new Edge(a, b, w));
        }

        // 1）按权重从小到大排序边集
        Collections.sort(edges);

        // 2）贪心，合并当前未并入的最小边
        int ans = 0, cnt = 0;  // cnt 保存并入的边数
        for (Edge e : edges) {
            int a = e.x, b = e.y, w = e.w;

            a = find(p, a);  b = find(p, b);
            if (a == b) continue; // 已在同一个并查集
            p[a] = b;  // 归入最小生成树T
            ans += w;  // 最小生成树T 的权重
            cnt ++ ;
        }

        // 如果可以得到最小生成树，肯定有 cnt == n - 1

        return ans;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

# 使用数组表示 Edge （推荐）

第一种模板需要编写一个 Edge 边类来表示邻接关系，这种方式的优点在于使用面向对象编程，但在一些时候却过于麻烦。

因此，可以使用数组来代替 Edge ，刚好 adjs 就表示这种邻接关系。在排序时，使用 Arrays.sort(edges, (e1, e2) -> e1[2] - e2[2]) 就可以按权重排序，方便很多，比上面的方法少写了 20 行代码！

    // 并查集（查找祖先）
    private int find(int[] p, int x) {
        if (p[x] != x) p[x] = find(p, p[x]);
        return p[x];
    }

    /**
        Kruskal 算法 —— 最小生成树算法
        参数：
          adjs:  邻接关系        adjs[i] = {ui, vi, wi} 表示 ui 到 vi 的边权为 wi,   0 <= ui, vi <= n - 1
          n:     节点数量
        返回值：
          ans:  最小生成树的权重
     */
    private int kruskal(int[][] adjs, int n) {
        int[] p = new int[n];  // 并查集，每个节点的祖先节点（用于并查集合并操作）
        
        for (int i = 0; i < n; ++ i ) p[i] = i;  // 开始时，所有边还没合并，祖先是自己

        // 边集
        int m = adjs.length, idx = 0;
        int[][] edges = new int[m][3];
        for (int[] adj : adjs) {
            int a = adj[0], b = adj[1], w = adj[2];
            edges[idx ++ ] = new int[]{a, b, w};
        }

        // 1）按权重从小到大排序边集
        Arrays.sort(edges, (e1, e2) -> e1[2] - e2[2]);

        // 2）贪心，合并当前未并入的最小边
        int ans = 0, cnt = 0;  // cnt 保存并入的边数
        for (int[] e : edges) {
            int a = e[0], b = e[1], w = e[2];

            a = find(p, a);  b = find(p, b);
            if (a == b) continue; // 已在同一个并查集
            p[a] = b;  // 归入最小生成树T
            ans += w;  // 最小生成树T 的权重
            cnt ++ ;
        }

        // 如果可以得到最小生成树，肯定有 cnt == n - 1

        return ans;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47

# 复杂度分析

复杂度分析
时间复杂度	$O(m \log(m))$ ，其中 $m$ 是边数
空间复杂度	$O(n^2)$ ，并查集使用 $O(n)$ 空间，边集数组使用 $O(n^2)$ 空间

# 同类题型

【最小生成树：Kruskal/Prim】

# 字典树/前缀树/Trie

# 题例

题例：208. 实现 Trie (前缀树)

Trie（发音类似 "try"）或者说前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。

void insert(String word) 向前缀树中插入字符串 word 。

boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。

boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

From LeetCode (opens new window)

# 模板

class Trie {

    class Node {
        boolean endPoint;
        Node[] son = new Node[26];
    }

    private Node root;  // 根节点

    public Trie() {
        this.root = new Node();
    }
    
    public void insert(String word) {
        Node p = root;
        for (char c : word.toCharArray()) {
            int u = c - 'a';
            // 如果当前字符不存在，则创建一个结点来保存
            if (p.son[u] == null) p.son[u] = new Node();
            // 进入下一个结点
            p = p.son[u];
        }
        p.endPoint = true;  // 作为结束点
    }
    
    public boolean search(String word) {
        Node p = root;
        for (char c : word.toCharArray()) {
            int u = c - 'a';
            // 如果当前字符不存在，表明 word 不存在 Trie 中
            if (p.son[u] ==  null) return false;
            // 进入下一个结点
            p = p.son[u];
        }
        return p.endPoint;
    }
    
    public boolean startsWith(String prefix) {
        Node p = root;
        for (char c : prefix.toCharArray()) {
            int u = c - 'a';
            // 如果当前字符不存在，表明 word 不存在 Trie 中
            if (p.son[u] ==  null) return false;
            // 进入下一个结点
            p = p.son[u];
        }
        return true;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

# 同类题型

# 动态规划

动态规划五步曲：

确定 dp 数组以及下标的含义
确定递归公式
dp 数组如何初始化
确定遍历顺序
举例推导 dp 数组

# 背包问题

# 01背包模板

二维数组版本

    /**
     * w[i] 第i个物品的重量， 0 <= i <= n, len(w) = n+1,  其中 w[0] 表示无物品
     * v[i] 第i个物品的价值， 0 <= i <= n, len(v) = n+1,  其中 w[0] 表示无价值
     *   m  背包容量
     *   n  物品数量
     * 返回值: 容量m下挑选n个物品的最大价值
     * */
    private int knapsack01(int n, int[] w, int[] v, int m) {
        int[][] f = new int[n + 1][m + 1];    // f[i][j] - 前 i 个物品中，容量为 j 的情况下，最大价值为 f[i][j]
                                      //         - 选第 i 个物品，则价值为 f[i - 1][j - w[i]] + v[i]
                                      //         - 不选 ... ，则价值从上一步转移，即 f[i - 1][j]
        
        for (int i = 1; i <= n; ++ i )  // 遍历第 i 个物品
            for (int j = 1; j <= m; ++ j ) {
                if (j < w[i]) f[i][j] = f[i - 1][j];                              // 不选时
                else f[i][j] = Math.max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);  // 要选时
            }
            
        return f[n][m];
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

滚动数组版本

    private int knapsack01(int n, int[] w, int[] v, int m) {
        int[] f = new int[m + 1];
        
        for (int i = 1; i <= n; ++ i )  // 遍历第 i 个物品
            for (int j = m; j >= w[i]; -- j ) {
                f[j] = Math.max(f[j], f[j - w[i]] + v[i]);  // 要选时
            }
            
        return f[m];
    }

1
2
3
4
5
6
7
8
9
10

# 完全背包模板

    private int completePack(int n, int[] w, int[] v, int m) {
        int[] f = new int[m + 1];
        
        // 遍历顺序可以调换
        for (int i = 1; i <= n; ++ i )  // 遍历第 i 个物品
            for (int j = w[i]; j <= m; ++ j )  // 遍历容量
                f[j] = Math.max(f[j], f[j - w[i]] + v[i]);
        
        return f[m];
    }

1
2
3
4
5
6
7
8
9
10

# 同类题型

灵茶山艾府 | 分享丨【题单】动态规划（入门/背包/状态机/划分/区间/状压/数位/树形/数据结构优化） (opens new window)

# 数学知识

# 素数/质数

# 模板（判断素数|筛素数|分解质因子）

# 判断素数

    // 判断素数（质数）
    private boolean isPrime(int n) {
        if (n < 2) return false;
        for (int i = 2; i <= n / i; ++ i )
            if (n % i == 0) return false;
        return true;
    }

1
2
3
4
5
6
7

# 筛素数

    // 求[1,n]内的素数  【方法1：普通筛法  O(nlogn)】
    private List<Integer> getPrimes(int n) {
        // primes 保存素数
        List<Integer> primes = new ArrayList<>();
        // st[i] 表示数i不是素数，则 st[i] 为 false 表示素数
        boolean[] st = new boolean[n + 1];
        st[0] = st[1] = true;

        for (int i = 2; i <= n; ++ i ) {
            // 当前的i为质数
            if (!st[i]) primes.add(i);
            // 不管是质数还是合数，都用来筛掉后面它的倍数
            for (int j = i + i; j <= n; j += i)
                st[j] = true;  
        }

        return primes;
    } 

    // 求[1,n]内的素数  【方法2：埃式筛法  O(nlog(logn))】
    private List<Integer> getPrimes_es(int n) {
        // primes 保存素数
        List<Integer> primes = new ArrayList<>();
        // st[i] 表示数i不是素数，则 st[i] 为 false 表示素数
        boolean[] st = new boolean[n + 1];
        st[0] = st[1] = true;

        for (int i = 2; i <= n; ++ i ) {
            // 当前的i为质数
            if (!st[i]) {
                primes.add(i);
                for (int j = i + i; j <= n; j += i)
                    st[j] = true;  // 除掉那些质数的倍数
            }
        }

        return primes;
    } 

    // 求[1,n]内的素数  【方法3：线性筛法  O(n)】
    private List<Integer> getPrimes_line(int n) {
        // primes 保存素数
        List<Integer> primes = new ArrayList<>();
        // st[i] 表示数i不是素数，则 st[i] 为 false 表示素数
        boolean[] st = new boolean[n + 1];
        st[0] = st[1] = true;

        for (int i = 2; i <= n; ++ i ) {
            // 当前的i为质数
            if (!st[i]) primes.add(i);
            // 去掉一些不满足条件的数
            for (int j = 0; primes.get(j) <= n / i; ++ j ) {
                st[i * primes.get(j)] = true;  // 用最小质因子去筛合数
                /*
                    - primes 数组中的素数是递增的，当i能整除primes[j]，那么i*primes[j+1]这个合数
                      肯定被primes[j]乘以某个数筛掉。
                    - 因为i中含有primes[j]，primes[j]比primes[j+1]小，
                      即i=k*primes[j]，那么i*primes[j+1]=(k*primes[j])*primes[j+1]=k’*primes[j]，
                      接下去的素数同理。所以不用筛下去了。
                    - 因此，在满足i%primes[j]==0这个条件之前以及第一次满足改条件时,
                      primes[j]必定是primes[j]*i的最小因子。
                */
                if (i % primes.get(j) == 0) break;
            }
        }

        return primes;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

# 分解质因子

    // 单计算一个数 n 的质因子
    // 返回值：列表，每一项表示数 n 的不同质因子及其数量
    private List<int[]> devide(int n) {
        // factors[i] 保存数字 n 的第i个质因子 factors[i][0] 及该质因子对应的数量 factors[i][1]
        List<int[]> factors = new ArrayList<>();  
        // 寻找质因子
        for (int i = 2; i <= n / i; ++ i ) {
            if (n % i == 0) {
                int s = 0;
                while (n % i == 0) {
                    ++ s;
                    n /= i;
                }
                factors.add(new int[]{i, s});
            }
        }
        // 循环结束后，添加剩余的质因数 
        if (n > 1) factors.add(new int[]{n, 1});

        return factors;
    }

    // 单计算一个数 n 的质因子
    // 返回值：集合，表示数字 n 的不同质因子
    private HashSet<Integer> devide(int n) {
        // 保存数字 n 的不同质因子 
        HashSet<Integer> factors = new HashSet<>();  
        // 寻找质因子
        for (int i = 2; i <= n / i; ++ i ) {
            if (n % i == 0) {
                while (n % i == 0) n /= i;
                factors.add(i);
            }
        }
        // 循环结束后，添加剩余的质因数 
        if (n > 1) factors.add(n);

        return factors;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

# 前述

# Java 算法常用

# 笔记&模板

# 二分查找

# 问题

# 解决方法

# 模板

# 三种写法

# 复杂度分析

# 同类题型

# 最短路算法

# Dijkstra 算法

# 算法思想

# 朴素 Dijkstra （适用于稠密图）

# 模板

# 复杂度分析

# 堆优化 Dijkstra （适用于稀疏图）

# 模板

# 复杂度分析

# Bellman Ford

# 模板

# 复杂度分析

# SPFA（BF 优先队列优化）

# 模板

# 复杂度分析

# Floyd 算法

# 算法思想

# 模板

# 复杂度分析

# 同类题型

# 最小生成树算法

# 题例

# Prim 算法

# 模板

# Kruskal 算法

# 算法思想

# 模板

# 使用 Edge 类

# 使用数组表示 Edge （推荐）

# 复杂度分析

# 同类题型

# 字典树/前缀树/Trie

# 题例

# 模板

# 同类题型

# 动态规划

# 背包问题

# 01背包模板

# 完全背包模板

# 同类题型

# 数学知识

# 素数/质数

# 模板（判断素数|筛素数|分解质因子）

# 判断素数

# 筛素数

# 分解质因子

# 快速幂